Heuristics

The mathematical problem described in Mathematical model can be solved using linear programming which is guaranteed to give the optimal solution. This can be computationally expensive, thus conference_scheduler includes the ability to search the solution space in an efficient manner to obtain if not the best solution: a very good one.

A good overview of the main ideas behind these types of algorithms can be found in [Aarts1997].

One subset of these types of algorithms is called neighbourhood searches. This involves defining a neighbourhood of a candidate solution. In conference_scheduler, the neighbourhood of a matrix \(X\) is defined as the matrix that corresponds to moving a single event to another slot. If the new slot is currently being used by another event the two events are swapped.

The general format of a neighbourhood search is to randomly select an element in the neighbourhood of \(X\) and either accept it or not as the new current solution according to a given criteria.

Hill climbing

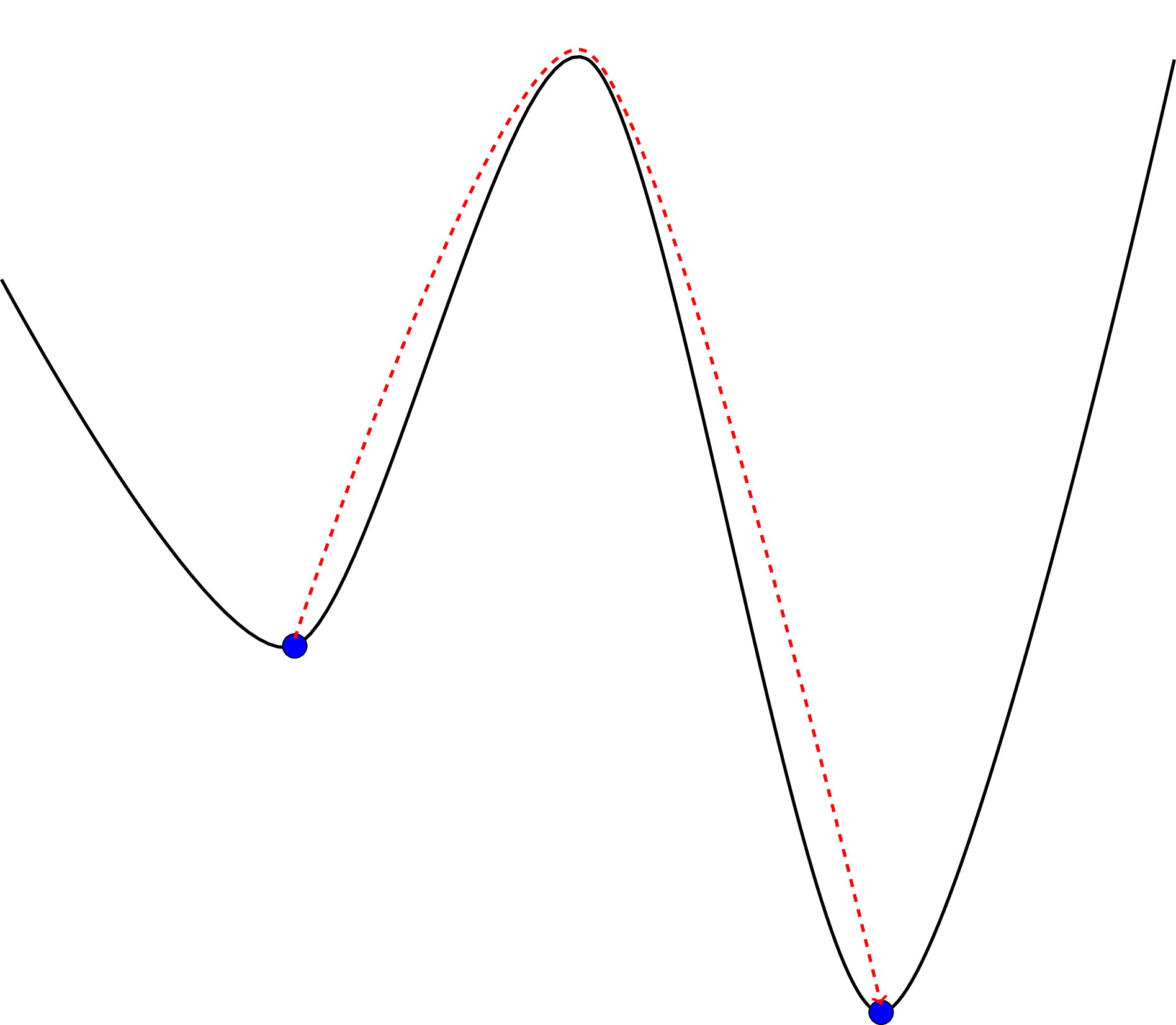
The Hill climbing algorithm has the most elementary acceptance criteria for a new solution. If the new solution has a better score then it is accepted.

The downside to this greedy approach is that by immediately accepting the better solution the algorithm can arrive at a local optimal: a hill top that is not the highest hill.

Note that the objective functions used in conference_scheduler are minimised. Whilst, mathematically this is equivalent, the analogy of finding the highest hill through hill climbing fails and we are in fact looking for the lowest valley.

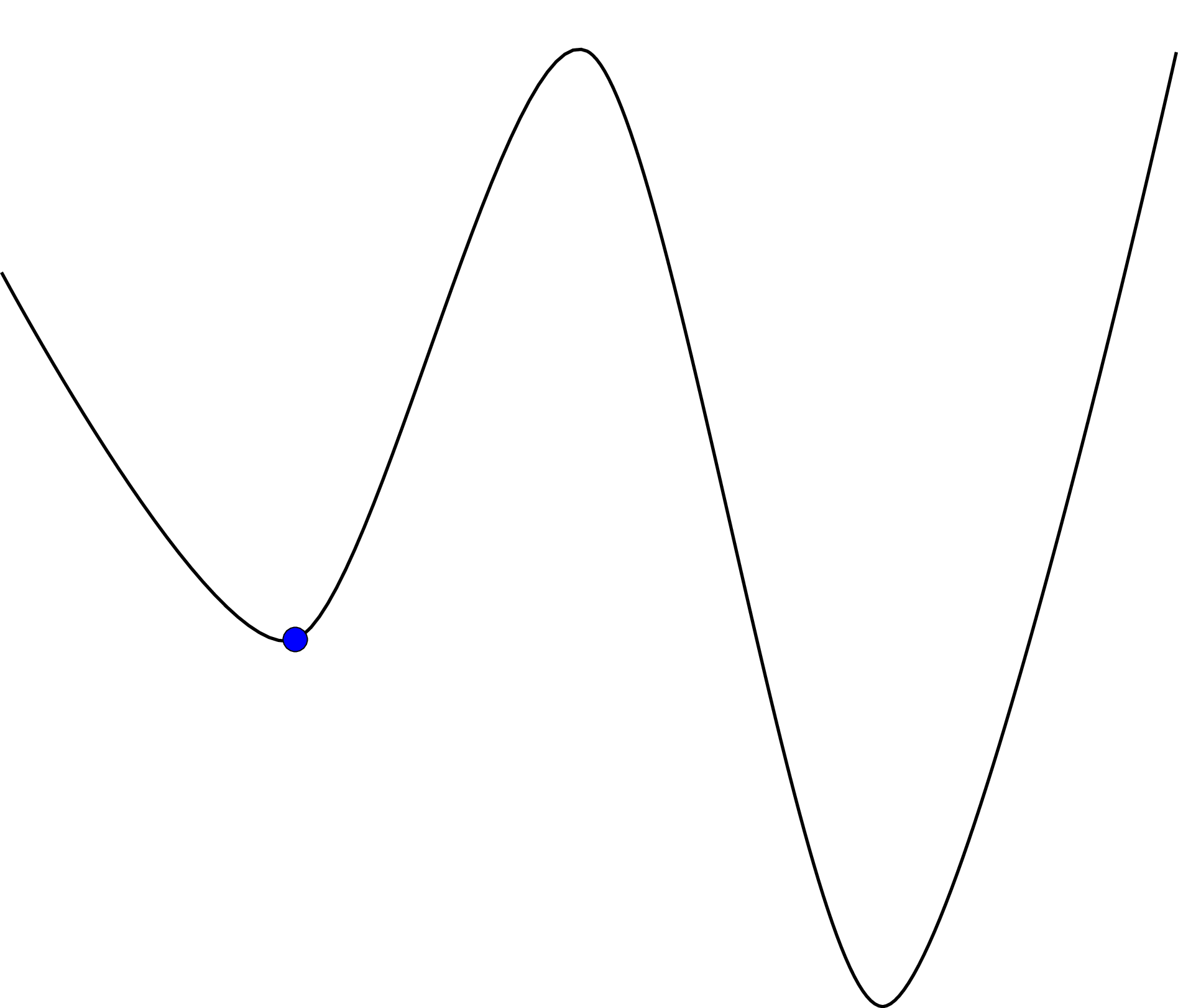
../_images/hill_climbing.png

Simulated annealing

This algorithm will accept a worse solution with a given probability. However this probability will decrease over time. Thus, the algorithm spends time at the beginning exploring the search space before beginning to hone in to a better solution. The name of this algorithm comes from the concept of annealing in metallurgy. A good overview of this is given in [Henderson2003].

This in essence allows our search to “jump” away from local optima.

../_images/simulated_annealing.png